Четырёхугольником называется геометрическая фигура, у которой есть четыре стороны и четыре угла.
Как пример, на рисунке ниже Вы видите фигуру EFGD.
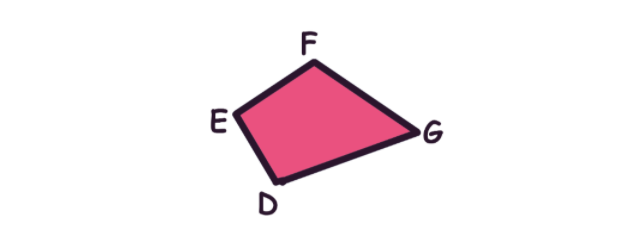
EFGD относится к произвольным четырёхугольникам. Да-да, четырёхугольники бывают очень разными!
Например, тот, у которого стороны равны между собой, а все углы прямые, называется квадратом. Вот он:


Помимо вышеперечисленных видов четырёхугольника существуют параллелограмм, трапеция, ромб. При всём многообразии фигур роднят их стороны, вершины и углы четырёхугольника, которых неизменно четыре.
Ознакомившись с теорией, предлагаем перейти к практике. Решим парочку задач с участием четырёхугольников.
Задача №1
Условие:
Для игры Костя вырезал 7 квадратов. Но спустя время понял, что одними квадратами не ограничится, поэтому добавил к ним 8 прямоугольников и 4 треугольника. Сколько четырёхугольников Костя использует в игре?
Решение:
Итак, все числа известны - в чём же загвоздка задачи? А в том, чтобы вспомнить, какие фигуры относятся к четырёхугольникам, а какие - нет. Рассуждаем:
- Квадрат. Содержит в себе четыре равные между собой стороны и четыре угла. Следовательно, это четырёхугольник.
- Прямоугольник. Состоит из четырёх сторон, параллельно равных друг другу. Также в прямоугольнике есть четыре прямых угла. Значит, это четырёхугольник.
- Треугольник. Видим “три” в самом названии и вспоминаем, что треугольником зовётся геометрическая фигура из трёх точек, не принадлежащих одной прямой. Точки эти соединены между собой отрезками, которые формируют три стороны и три угла между собой. Очевидно, что треугольник не относится к четырёхугольникам.
Разобравшись, мы можем сложить только те фигуры, которые требует от нас условие задачи - квадраты и прямоугольники.
7 + 8 = 15 (четырёхугольников) - используется в Костиной игре.
Ответ: 15 четырёхугольников.
Задача №2
Условие:
Марина начертила 6 прямоугольников. А Виталик - квадраты, которых получилось на 5 штук больше, чем прямоугольников у Марины. Сколько четырёхугольников изобразили школьники вместе?
Решение:
Найдём количество квадратов, которые начертил Виталик:
6 + 5 = 11
Теперь, когда нам известны необходимые для решения числа, проверим, все ли фигуры являются четырёхугольниками.
- Прямоугольник - да;
- Квадрат - да.
Остаётся только найти сумму:
6 + 11 = 17 (четырёхугольников) - изобразили Марина и Виталик вместе.
Ответ: 17 четырёхугольников.
Мы отлично справились! Но это лишь малая часть того, что подготовили преподаватели WoM для Вашего ребёнка. Обилие примеров и задач на тему “Четырёхугольник” ждут юного математика на уроке в онлайн-школе.
Записаться на бесплатное занятие можно здесь








